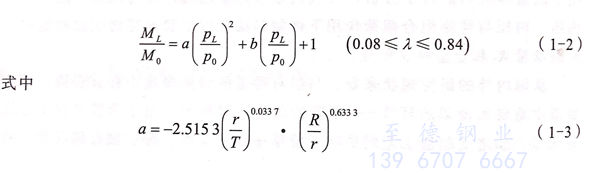1911年,德國科學家Van Karman首先用最小應變能方法研究了久久99國產精品久久99果凍傳媒:不銹鋼管彎管加工后的應力應變特性,之后的一些學者都以此方法為基礎,僅在級數的取舍等方面作了改進。Clark則認為彎管段為封閉環殼的一部分,通過薄殼方程并以兩個變量來表達這些方程,其解與已有解非常接近,且數學處理十分成功,但上述都僅限于彎曲半徑較大的情形。Pardue和Vigness,還有 Turner、Ford都研究了彎曲半徑較小的情形,給出了整個彎管截面的應力曲線。直到1956年,Kafla和Dunn注意到內壓對柔度系數的影響,指出了內壓可使彎管的柔度系數降低,剛度增大。Rodabaugh 和 George 利用能量方法研究了內壓的影響,給出了影響計算的理論公式。Clark等的計算公式和Rodabaugh等的內壓影響修正公式現在被各國規范所廣泛使用。
我國(guo)在(zai)(zai)(zai)“八五(wu)”“九(jiu)五(wu)”科技(ji)(ji)攻關(guan)期間,已基本解(jie)決了(le)(le)(le)(le)壓(ya)(ya)(ya)力(li)(li)容(rong)器、壓(ya)(ya)(ya)力(li)(li)管(guan)道直管(guan)段的(de)(de)(de)(de)(de)(de)(de)(de)塑性(xing)極(ji)限(xian)(xian)載(zai)(zai)(zai)(zai)荷(he)(he)(he)(he)計(ji)(ji)算(suan)及(ji)工(gong)程評估問題,但未涉及(ji)彎(wan)(wan)管(guan)等復(fu)雜(za)結(jie)(jie)構(gou)(gou)。鑒于其(qi)對(dui)(dui)管(guan)道系(xi)統(tong)承載(zai)(zai)(zai)(zai)能(neng)力(li)(li)的(de)(de)(de)(de)(de)(de)(de)(de)重(zhong)要影響,國(guo)家(jia)(jia)科技(ji)(ji)部將壓(ya)(ya)(ya)力(li)(li)管(guan)道元(yuan)件(jian)的(de)(de)(de)(de)(de)(de)(de)(de)安(an)全(quan)評估技(ji)(ji)術列入(ru)“十五(wu)”國(guo)家(jia)(jia)重(zhong)大科技(ji)(ji)攻關(guan)的(de)(de)(de)(de)(de)(de)(de)(de)相關(guan)項目中。文(wen)獻(xian)給(gei)出(chu)了(le)(le)(le)(le)薄(bo)壁彎(wan)(wan)管(guan)的(de)(de)(de)(de)(de)(de)(de)(de)理(li)論(lun)解(jie),文(wen)獻(xian)采(cai)用(yong)(yong)(yong)數(shu)值(zhi)分(fen)析(xi)的(de)(de)(de)(de)(de)(de)(de)(de)方(fang)(fang)法,對(dui)(dui)不(bu)銹鋼彎(wan)(wan)管(guan)結(jie)(jie)構(gou)(gou)在(zai)(zai)(zai)復(fu)雜(za)載(zai)(zai)(zai)(zai)荷(he)(he)(he)(he)作(zuo)(zuo)用(yong)(yong)(yong)下(xia)的(de)(de)(de)(de)(de)(de)(de)(de)極(ji)限(xian)(xian)與(yu)安(an)定(ding)分(fen)析(xi)進行(xing)了(le)(le)(le)(le)深入(ru)、系(xi)統(tong)的(de)(de)(de)(de)(de)(de)(de)(de)研(yan)究,發展了(le)(le)(le)(le)多(duo)組(zu)載(zai)(zai)(zai)(zai)荷(he)(he)(he)(he)作(zuo)(zuo)用(yong)(yong)(yong)下(xia)不(bu)銹鋼管(guan)彎(wan)(wan)管(guan)結(jie)(jie)構(gou)(gou)塑性(xing)極(ji)限(xian)(xian)上限(xian)(xian)分(fen)析(xi)的(de)(de)(de)(de)(de)(de)(de)(de)有限(xian)(xian)元(yuan)數(shu)學規(gui)劃方(fang)(fang)法,得(de)出(chu)了(le)(le)(le)(le)相應的(de)(de)(de)(de)(de)(de)(de)(de)無搜(sou)索優化(hua)迭代求解(jie)算(suan)法,給(gei)出(chu)了(le)(le)(le)(le)可較好地解(jie)決復(fu)雜(za)載(zai)(zai)(zai)(zai)荷(he)(he)(he)(he)作(zuo)(zuo)用(yong)(yong)(yong)下(xia)彎(wan)(wan)管(guan)結(jie)(jie)構(gou)(gou)與(yu)安(an)定(ding)分(fen)析(xi)的(de)(de)(de)(de)(de)(de)(de)(de)數(shu)值(zhi)算(suan)法。文(wen)獻(xian)就(jiu)含(han)局(ju)部減(jian)薄(bo)彎(wan)(wan)管(guan)的(de)(de)(de)(de)(de)(de)(de)(de)極(ji)限(xian)(xian)載(zai)(zai)(zai)(zai)荷(he)(he)(he)(he)作(zuo)(zuo)了(le)(le)(le)(le)研(yan)究,得(de)出(chu)了(le)(le)(le)(le)含(han)局(ju)部減(jian)薄(bo)彎(wan)(wan)管(guan)的(de)(de)(de)(de)(de)(de)(de)(de)極(ji)限(xian)(xian)載(zai)(zai)(zai)(zai)荷(he)(he)(he)(he)的(de)(de)(de)(de)(de)(de)(de)(de)工(gong)程計(ji)(ji)算(suan)方(fang)(fang)法;文(wen)獻(xian)對(dui)(dui)在(zai)(zai)(zai)拉、壓(ya)(ya)(ya)、彎(wan)(wan)、扭和內(nei)(nei)(nei)(nei)壓(ya)(ya)(ya)作(zuo)(zuo)用(yong)(yong)(yong)下(xia)含(han)缺(que)陷(xian)彎(wan)(wan)管(guan)的(de)(de)(de)(de)(de)(de)(de)(de)極(ji)限(xian)(xian)載(zai)(zai)(zai)(zai)荷(he)(he)(he)(he)作(zuo)(zuo)了(le)(le)(le)(le)研(yan)究,得(de)出(chu)了(le)(le)(le)(le)彎(wan)(wan)管(guan)在(zai)(zai)(zai)組(zu)合載(zai)(zai)(zai)(zai)荷(he)(he)(he)(he)作(zuo)(zuo)用(yong)(yong)(yong)下(xia)的(de)(de)(de)(de)(de)(de)(de)(de)極(ji)限(xian)(xian)載(zai)(zai)(zai)(zai)荷(he)(he)(he)(he)的(de)(de)(de)(de)(de)(de)(de)(de)計(ji)(ji)算(suan)公式,能(neng)滿足(zu)一般(ban)工(gong)程的(de)(de)(de)(de)(de)(de)(de)(de)計(ji)(ji)算(suan)。文(wen)獻(xian)對(dui)(dui)環(huan)向(xiang)(xiang)(xiang)穿透裂(lie)紋(wen)的(de)(de)(de)(de)(de)(de)(de)(de)斜(xie)接彎(wan)(wan)管(guan)進行(xing)了(le)(le)(le)(le)有限(xian)(xian)元(yuan)分(fen)析(xi),計(ji)(ji)算(suan)給(gei)出(chu)了(le)(le)(le)(le)線彈性(xing)條件(jian)下(xia),焊制斜(xie)接彎(wan)(wan)管(guan)環(huan)向(xiang)(xiang)(xiang)穿透裂(lie)紋(wen)分(fen)別在(zai)(zai)(zai)內(nei)(nei)(nei)(nei)壓(ya)(ya)(ya)、彎(wan)(wan)矩(ju)(ju)載(zai)(zai)(zai)(zai)荷(he)(he)(he)(he)作(zuo)(zuo)用(yong)(yong)(yong)下(xia)斷(duan)裂(lie)參(can)量(liang)(liang)K1的(de)(de)(de)(de)(de)(de)(de)(de)工(gong)程應用(yong)(yong)(yong)解(jie);同時以(yi)內(nei)(nei)(nei)(nei)壓(ya)(ya)(ya)、彎(wan)(wan)矩(ju)(ju)不(bu)同比(bi)例的(de)(de)(de)(de)(de)(de)(de)(de)載(zai)(zai)(zai)(zai)荷(he)(he)(he)(he)比(bi)作(zuo)(zuo)用(yong)(yong)(yong)下(xia)求解(jie)出(chu)全(quan)塑性(xing)J積分(fen)值(zhi)。文(wen)獻(xian)對(dui)(dui)沿(yan)管(guan)向(xiang)(xiang)(xiang)穿透裂(lie)紋(wen)的(de)(de)(de)(de)(de)(de)(de)(de)斜(xie)接彎(wan)(wan)管(guan)在(zai)(zai)(zai)內(nei)(nei)(nei)(nei)壓(ya)(ya)(ya)、彎(wan)(wan)矩(ju)(ju)聯合作(zuo)(zuo)用(yong)(yong)(yong)下(xia)的(de)(de)(de)(de)(de)(de)(de)(de)整體(ti)應力(li)(li)進行(xing)了(le)(le)(le)(le)分(fen)析(xi),并利用(yong)(yong)(yong)斷(duan)裂(lie)力(li)(li)學的(de)(de)(de)(de)(de)(de)(de)(de)理(li)論(lun)和有限(xian)(xian)元(yuan)方(fang)(fang)法計(ji)(ji)算(suan)了(le)(le)(le)(le)內(nei)(nei)(nei)(nei)壓(ya)(ya)(ya)、內(nei)(nei)(nei)(nei)壓(ya)(ya)(ya)與(yu)彎(wan)(wan)矩(ju)(ju)組(zu)合載(zai)(zai)(zai)(zai)荷(he)(he)(he)(he)作(zuo)(zuo)用(yong)(yong)(yong)下(xia)焊制斜(xie)接彎(wan)(wan)管(guan)沿(yan)管(guan)向(xiang)(xiang)(xiang)穿透裂(lie)紋(wen)的(de)(de)(de)(de)(de)(de)(de)(de)線彈性(xing)斷(duan)裂(lie)參(can)量(liang)(liang) K1和全(quan)塑性(xing)J積分(fen)。
從國內外的(de)(de)(de)研(yan)究(jiu)現(xian)狀來(lai)看,目前對(dui)不(bu)銹(xiu)鋼(gang)管(guan)(guan)(guan)(guan)道(dao)的(de)(de)(de)研(yan)究(jiu)多(duo)集(ji)中在直(zhi)管(guan)(guan)(guan)(guan)段,圍繞管(guan)(guan)(guan)(guan)道(dao)中重要(yao)而薄弱(ruo)的(de)(de)(de)環節-彎(wan)(wan)(wan)(wan)管(guan)(guan)(guan)(guan)的(de)(de)(de)研(yan)究(jiu)相對(dui)較(jiao)少。由于彎(wan)(wan)(wan)(wan)管(guan)(guan)(guan)(guan)幾(ji)何中心線(xian)(xian)是曲線(xian)(xian),加(jia)(jia)之受(shou)制(zhi)(zhi)造工藝的(de)(de)(de)影響,管(guan)(guan)(guan)(guan)壁(bi)往往不(bu)等厚(hou)(hou)(hou),存在截面(mian)橢圓化(hua),外拱(gong)壁(bi)厚(hou)(hou)(hou)局(ju)部變(bian)(bian)薄,內拱(gong)壁(bi)厚(hou)(hou)(hou)局(ju)部變(bian)(bian)厚(hou)(hou)(hou)甚至出現(xian)皺褶等缺陷(xian),當受(shou)到(dao)內壓(ya)(ya)和(he)彎(wan)(wan)(wan)(wan)矩的(de)(de)(de)聯合作用(yong)時,幾(ji)何和(he)材(cai)料的(de)(de)(de)非線(xian)(xian)性相互作用(yong),使得彎(wan)(wan)(wan)(wan)管(guan)(guan)(guan)(guan)的(de)(de)(de)應(ying)力(li)狀態比直(zhi)管(guan)(guan)(guan)(guan)復(fu)(fu)雜(za),因(yin)而研(yan)究(jiu)起來(lai)也(ye)相對(dui)復(fu)(fu)雜(za)。而對(dui)超高(gao)壓(ya)(ya)彎(wan)(wan)(wan)(wan)管(guan)(guan)(guan)(guan)還要(yao)涉及彎(wan)(wan)(wan)(wan)管(guan)(guan)(guan)(guan)的(de)(de)(de)應(ying)力(li)沿壁(bi)厚(hou)(hou)(hou)分布不(bu)均(jun)勻和(he)應(ying)力(li)集(ji)中的(de)(de)(de)現(xian)象(xiang),因(yin)而對(dui)超高(gao)壓(ya)(ya)彎(wan)(wan)(wan)(wan)管(guan)(guan)(guan)(guan)的(de)(de)(de)研(yan)究(jiu)就更加(jia)(jia)復(fu)(fu)雜(za),目前對(dui)超高(gao)壓(ya)(ya)彎(wan)(wan)(wan)(wan)管(guan)(guan)(guan)(guan)的(de)(de)(de)研(yan)究(jiu)文(wen)獻資料報道(dao)得很(hen)少,而現(xian)有的(de)(de)(de)文(wen)獻資料報道(dao)得最多(duo)的(de)(de)(de)是超高(gao)壓(ya)(ya)彎(wan)(wan)(wan)(wan)管(guan)(guan)(guan)(guan)的(de)(de)(de)加(jia)(jia)工與(yu)制(zhi)(zhi)造工藝,對(dui)超高(gao)壓(ya)(ya)彎(wan)(wan)(wan)(wan)管(guan)(guan)(guan)(guan)的(de)(de)(de)受(shou)力(li)分析及工程中的(de)(de)(de)應(ying)用(yong)的(de)(de)(de)研(yan)究(jiu)報道(dao)只(zhi)有楊家瑞在文(wen)獻中提到(dao)了超高(gao)壓(ya)(ya)彎(wan)(wan)(wan)(wan)管(guan)(guan)(guan)(guan)的(de)(de)(de)極(ji)限(xian)載荷的(de)(de)(de)計算方法。2010年(nian),毛(mao)苗等人(ren)對(dui)受(shou)內壓(ya)(ya)作用(yong)下的(de)(de)(de)90度(du)大型(xing)厚(hou)(hou)(hou)壁(bi)彎(wan)(wan)(wan)(wan)管(guan)(guan)(guan)(guan)進(jin)行了應(ying)力(li)計算分析及試驗研(yan)究(jiu),得到(dao)了彎(wan)(wan)(wan)(wan)管(guan)(guan)(guan)(guan)的(de)(de)(de)應(ying)力(li)分布規律。2011年(nian),樂(le)增等人(ren)應(ying)用(yong)雙剪強度(du)理(li)論推導出求(qiu)解不(bu)銹(xiu)鋼(gang)管(guan)(guan)(guan)(guan)彎(wan)(wan)(wan)(wan)管(guan)(guan)(guan)(guan)的(de)(de)(de)極(ji)限(xian)載荷一般公式(shi),如式(shi)(1-1)所示。

2014年(nian),朱倩(qian)等(deng)人基于統(tong)一(yi)強(qiang)度(du)理論(lun),考慮(lv)中(zhong)間(jian)主應(ying)(ying)力效應(ying)(ying)及(ji)(ji)拉壓(ya)不(bu)等(deng)特性(xing),建立了等(deng)壁厚、變壁厚及(ji)(ji)局部減薄壓(ya)力彎(wan)(wan)(wan)管(guan)(guan)的(de)(de)極限內(nei)壓(ya)統(tong)一(yi)解(jie)(jie),研究了統(tong)一(yi)強(qiang)度(du)理論(lun)參數(shu)、拉壓(ya)比、彎(wan)(wan)(wan)曲系數(shu)和不(bu)銹鋼(gang)管(guan)(guan)彎(wan)(wan)(wan)管(guan)(guan)壁厚對(dui)統(tong)一(yi)解(jie)(jie)的(de)(de)影(ying)響特性(xing),結果(guo)表明:彎(wan)(wan)(wan)曲系數(shu)、強(qiang)度(du)理論(lun)參數(shu)等(deng)因(yin)素對(dui)極限內(nei)壓(ya)曲線的(de)(de)影(ying)響顯(xian)著,考慮(lv)中(zhong)間(jian)主應(ying)(ying)力效應(ying)(ying)能(neng)充分發揮(hui)材料(liao)的(de)(de)強(qiang)度(du)潛(qian)能(neng)。李建等(deng)人考慮(lv)幾(ji)何和材料(liao)的(de)(de)非線性(xing)相互(hu)作(zuo)(zuo)用,采用有(you)限元方法研究了復雜載荷(he)下不(bu)銹鋼(gang)彎(wan)(wan)(wan)管(guan)(guan)的(de)(de)極限載荷(he),提出了彎(wan)(wan)(wan)矩以及(ji)(ji)內(nei)壓(ya)、彎(wan)(wan)(wan)矩聯合作(zuo)(zuo)用下的(de)(de)極限壓(ya)力、極限彎(wan)(wan)(wan)矩與(yu)彎(wan)(wan)(wan)管(guan)(guan)幾(ji)何尺寸的(de)(de)定量關系如式(1-2)。